Dopo aver visto come calcolare la resistenza a trazione di progetto nell'articolo vetro strutturale - resistenza del materiale oggi vediamo come modellare lastre di vetro con particolare attenzione alle lastre in vetro temperato stratificato.
 |
| Modellazione di una lastra di vetro stratificato con agganci puntuali |
Carichi di durata diversa
Il vetro è soggetto al fenomeno della “fatica statica” cioè subisce una progressiva diminuzione della resistenza a trazione quando è sottoposto ad un carico costante nel tempo. È quindi necessario considerare valori differenti di resistenza per differenti tempi di durata dei carichi inserendo un coefficente riduttivo detto Kmod.
Valori di Kmod
| Azione | Durata carichi | Kmod |
| Vento, Folla | 5 secondi | 1,00 |
| Neve | 6 settimane | 0,43 |
| Peso proprio | 50 anni | 0,29 |
| Var. temperatura giornaliera | 11 ore | 0,57 |
| Var. temperatura rara | 6 mesi | 0,38 |
| Var. di pressione | 4 giorni | 0,50 |
Per tener conto di questo fenomeno e quindi fare una verifica con carichi di durata diversa e, di conseguenza di resistenze diverse, si possono utilizzare questidue metodi:
- Si amplificano tutti i carichi non istantanei dividendoli per Kmod per poi effetturare la verifica utilizzando la resistenza per carichi istantanei. Esempio: il peso proprio di una lastra di 5 mm è 0,125 kN/mq, per tener conto dell'effetto della fatica statica del vetro viene amplificato di 1/Kmod cioè 0,125/0,29=0,431kN/mq. Il carico permanente viene più che triplicato. (metodo più cautelativo)
- Si inseriscono nel modello i carichi effettivi e si effettua una verifica combinando le varie sollecitazioni normalizzate:
Modellazione di lastre in vetro temperato stratificato
La difficoltà nella modellazione di elementi in vetro stratificato deriva dal fatto che le caratteristiche del PVB (Polivinilbutirrale) il materiale plastico che viene utilizzato tra le lastre di vetro che compongono l'elemento.
"La rigidezza globale dell’elemento stratificato è funzione, oltre che delle grandezze consuete, anche della capacità del PVB di trasmettere azioni di taglio tra le facce adiacenti dell’elemento stratificato" (Zenkert, D.;1997).
La capacità del PVB di trasmetere azioni taglianti cambia rapidamente al variare della temperatura: se a temperature vicine allo zero il comportamento del vetro multistrato è assimilabile a quello di una lastra omogenea già a 30/40 gradi il modulo G del PVB cala drasticamente non assicurando il trasferimento degli sforzi. Per questo modivo una modellazione rigorosa dei vari strati risulta molto difficile. Quella che propongo adesso è una modellazione semplice, veloce ed a favore di sicurezza proposta dalla Saint- Gobain nel 2003.
Caratteristiche meccaniche vetro
Modulo Elastico= 70000
MPa Coefficente di Poisson= 0,22
Densità= 2500 kg/mc
Caratteristiche meccaniche vetro
Modulo Elastico= 70000
MPa Coefficente di Poisson= 0,22
Densità= 2500 kg/mc
Modello a spessori equivalenti
Vengono impiegati elementi “shell”o "brick" comunemente adottati da tutti i codici di calcolo in cui lo spessore della piastra è assegnato opportunamente dall’utente. Le ipotesi sono:
- lo strato di PVB non è in grado di trasmettere alcuno sforzo di taglio, le lastre che compongono il vetro stratificato agiscono indipendentemente tra loro;
- gli spostamenti fuori dal piano sono uguali per i singoli strati;
- lo spessore equivalente per gli spostamenti consente di descrivere il campo dispostamenti della struttura;
- lo spessore equivalente per le tensioni consente di descrivere il campo tensionale dei singoli strati di vetro.
Spessore equivalente per gli spostamenti
Lo spessore equivalente per gli spostamenti è definito come quello spessore da assegnare alla piastra monolitica per avere gli stessi spostamenti della piastra stratificata in cui si considera il materiale di interfaccia incapace di trasmettere azioni di taglio.
L'altezza dello spessore equivalente per gli spostamenti è dato dalla formula:
dove hn è lo spessone della singola lastra. Per esempio per una lastra 10+1,52+10mm ottieniamo uno spessore equivalente per gli spostamenti pari a 12.60mm.
 |
| Spostamenti allo stato limite di esercizio |
Lo spessore equivalente per le sollecitazioni è definito come quello spessore da assegnare alla piastra monolitica per avere le stesse sollecitazioni della piastra stratificata in cui si considera il materiale di interfaccia incapace di trasmettere azioni di taglio.
L'altezza dello spessore equivalente per le sollecitazioni per la lastra k-esima è dato dalla formula:
Per esempio per la stessa lastra 10+1,52+10mm otteniamo uno spessore equivalente per le sollecitazioni pari a 14.14mm.
 |
| Tensioni principali allo stato limite ultimo
Per calcolare gli spessori equivalenti potete scaricare il foglio di calcolo ecxel Calcolo spessori equivalenti vetro crearo da me.
Qui potete trovare un esempio di come condurre calcolo e verifiche: Esempio di calcolo di un pavimento in vetro. |
A presto, Braian
Riferimenti:
Comportamento meccanico di lastre inflesse in vetro stratificato, Ing. Leonardo Lani


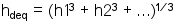

Il metodo proposto di combinazione delle tensioni nella verifica si semplifica se anziché normalizzare le tensioni si normalizzano i carichi.
RispondiEliminaIn questo modo si può eseguire un unico calcolo con i comuni programmi.
Calcolo di una lastra di vetro
ho visto il tuo link, considerando le lastre separate in parallelo giustamente su suddivide il carico in parti eguali per ogni lastra. numericamente questo calstracolo per 3 lastre di5mm mi da un risultato che ritengo accettabile. invece con le formule Saint gobain degli spessori equivalenti si arriva ad un assurdo: cioè che 3 lastre tificate con pvb resisterebbero meno di 3 lastre in parallelo aventi un terzo del carico ognuna.quelle formule sono troppo a favore di sicurezza, bisogna trovare un altro modo di calcolare gli spessori equivalenti.
Eliminasono d'accordo, normalizzare i carichi moltiplicandoli per Kmod è il metodo più veloce per procedere però volendo essere precisi si vede che nella formula per il calcolo della tensione massima a trazione il kmod viene moltiplicato solo per una parte della resistenza caratteristica (quella della tempera non viene ridotta) quindi normalizzando i carichi si "rinuncia" ad un pò di capacità del vetro. Resta comunque un ottimo metodo rapido ed a favore di sicurezza.
RispondiEliminaE per le vetrocamere come si fa?
RispondiEliminaE per le vetrocamere a fissaggio puntuale?
Me lo sonn posto anche io il problema vetrocamera: ho visto che i vetrocamera hanno solo uno dei due vetri stratificati (ho controllato le principali ditte della mia zona) e quindi io considero solo la lastra di vetro stratificato nel calcolo.
RispondiEliminaBuongiorno Stefano,io modellerei con elementi bidimensionali la lastra di vetro facendo due modelli con il metodo degli spessori equivalenti come spiegato in questo articolo. Qui trovi un esempio: http://www.ingegneriaedintorni.com/2011/02/esempio-di-calcolo-di-un-pavimento-in.html
RispondiEliminaUna domanda riguardo il foglio excel per il calcolo della resistenza del vetro. Perchè la tensione resistente allo SLU è inferiore a quella allo SLE (il gamma M passa da 1,4 a 1)?
RispondiEliminaDeriva dalle indicazioni sulle normative.
EliminaE' una domanda che mi sono posto pure io, non ti so rispondere.
Buongiorno,
RispondiEliminauna domanda riguardo lo spessore equivalente per le sollecitazioni. In caso di strati di spessori differenti la formula non mi da un unico valore, e già questo non lo capisco, dovendo trovare lo spessore di una lastra monolitica equivalente mi aspetto un unico valore.
Quindi, per esempio nel caso di un 10+5 ho come valori 12.3 e 13.8. Quale valore do alla lastra monolitica equivalente per la verifica?
Grazie
Per il calcolo della deformazione avrò un univo spessore che uso per calcolare l'abbassamento del sistema a più lastre.
EliminaPer il calcolo delle tensioni ho un diverso spessore per ogni lastra essendo queste ultime sollecitate in maniera diversa in base alla loro rigidezza (quindi spessore)
Nel caso di spessori differenti, per il calcolo delle tensioni si modellano le singole lastre con elementi shell con spessori differenti e si collegano le lastre con elementi link?
EliminaInoltre che differenza c'è tra tempra e tempra parziale. Il vetrario mi da vetri temprati senza specificare se sia parziale o meno.
RispondiEliminaGrazie
Saluti
Qui devi parlare con il vetraio, quando io non ho indicazioni più precise addotto per il calcolo in maniera cautelativa l'ipotesi di tempra parziale.
EliminaBraian.
Questo blog mi sta aiutando moltissimo nello svolgimento della mia tesi.
RispondiEliminaGrazie mille e complimenti!
Erica
Mi fa molto piacere erica, complimenti per il traguardo che stai per raggiungere!
Eliminabuonasera,
RispondiEliminase ho uno stratificato con diversi spessori, ottengo diversi spessori equivalenti (per le tensioni), uno per ogni strato.
Dovrò poi verificare i singoli strati con il relativo spessore equivalente, ma con quale carico? Verifico ogni lastra per il carico totale? Oppure per una frazione del carico totale (se 3 strati divido per 3 il carico totale)?
Grazie
Che tipo di programma hai utilizzato per i brick?
RispondiEliminaInoltre che vincoli sono stati inseriti dove si hanno gli agganci? Vincolo puntuale in un nodo?
Buonasera,
RispondiEliminaper il calcolo Spessore equivalente per le sollecitazioni mi chiedo come ottenete 14.14, io mi trovo:
10^3=1000, 1.52^3=3.5118
(1000/10 + 3.5118/1.52 + 1000/10 ) ^ 0.5 = 14.22 dove sbaglio?
per la verifica tensionale utilizzo questo spessore per gli shell, mentre per la verifica di deformabilità utilizzo lo spessore equivalente per gli spostamenti?
Grazi